Order Analysis
Order analysis is a set of functions for converting a signal from time-domain (i.e. signal sampled at discrete time intervals) into the order-domain (i.e. signal sampled at constant angular increments of a reference rotating device).
The purpose of this transformation is to provide a better distinction between signal artefacts introduced through a shaft rotation from other artefacts, and to better relate each spectral component to the shaft rotation speed.
In order to perform this transformation, a separate signal containing RPM (revolutions-per-minute) values is needed. This signal does not have to be sampled at the same sampling rate as the time signal, but the duration (in seconds) of both time signal and RPM signal should be approximately the same (+/-10%). If your revolution speed signal is in some other unit, for example, revolutions-per-seconds, you can easily convert it to RPM by using the “Scale/Normalise” function or the “Signal Calculator”.
SIGVIEW also includes functions to perform the inverse order transformation, i.e. to convert order-signal back into time-signal.
All order analysis functions (forward and inverse transformation) can be found in the Signal calculator:
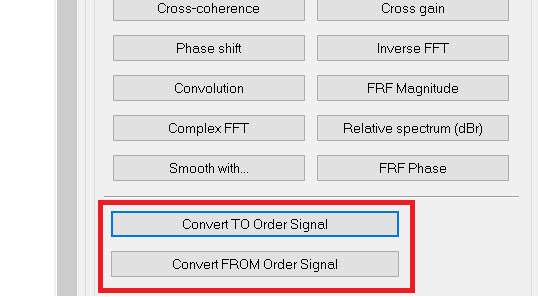
Example
For example, let us take a look at the spectrogram of the acceleration signal from a machine running at a changing shaft rotation speed. The spectrogram shows various artefacts which are obviously caused by the main shaft rotation speed changes, as shown in the corresponding RPM signal below.
Time domain signal (acceleration):
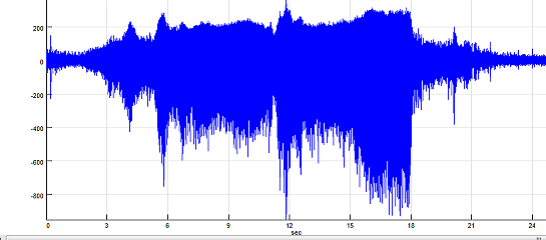
RPM signal:

Spectrogram:
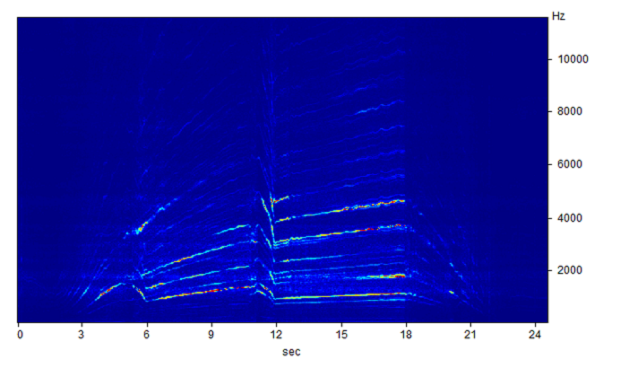
By using the Signal calculator, we can convert the original time-signal into the order signal. To do so, select the input vibration signal, then select the "Convert TO Order signal" function, and finally, add the RPM signal to the expression:
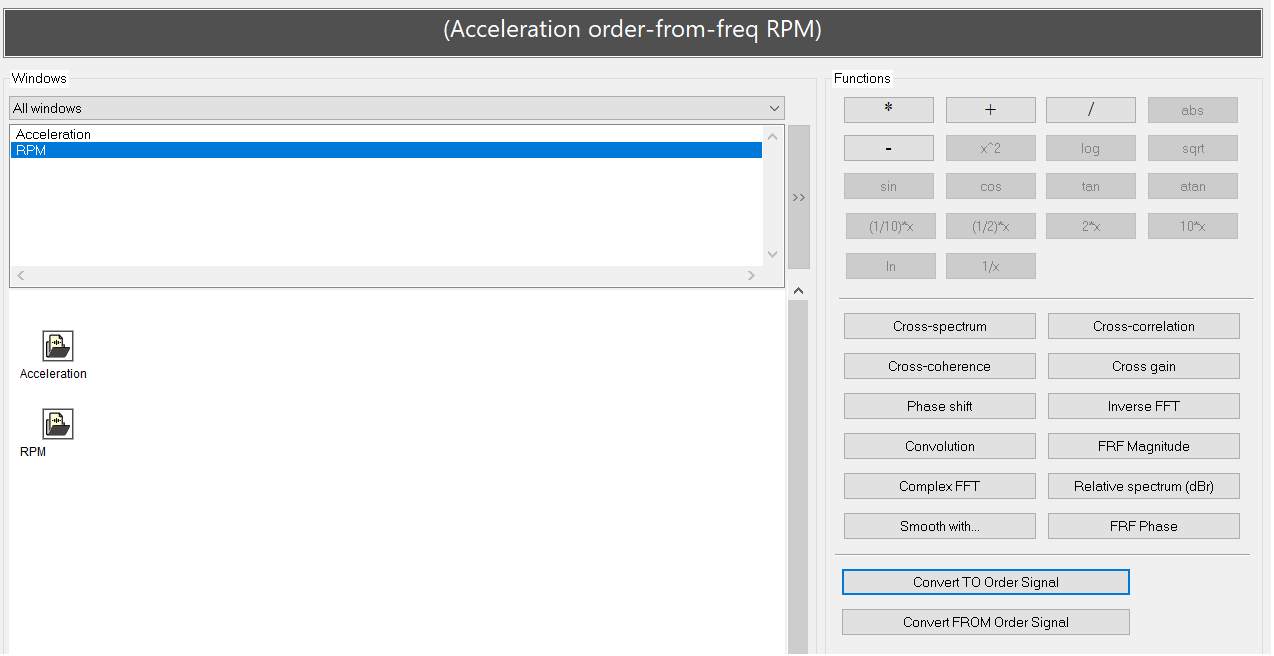
The result will be a signal, similar to the original time-domain signal, but with the X-axis in "revolutions" units instead of seconds. You can work with this signal just as with any other time-domain signal. For example, you can calculate its FFT, Spectrogram, Time-FFT... Just remember that the base for this signal is not "samples/sec" but "samples/shaft revolution"
Order signal:
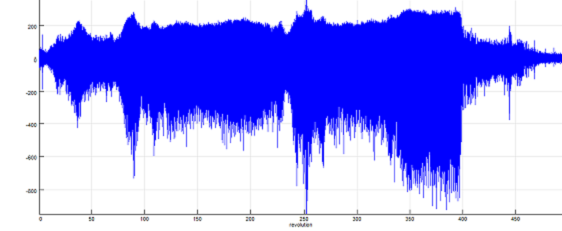
For example, if you calculate the spectrogram of the generated order-signal, you will get this result:
Order spectrogram:
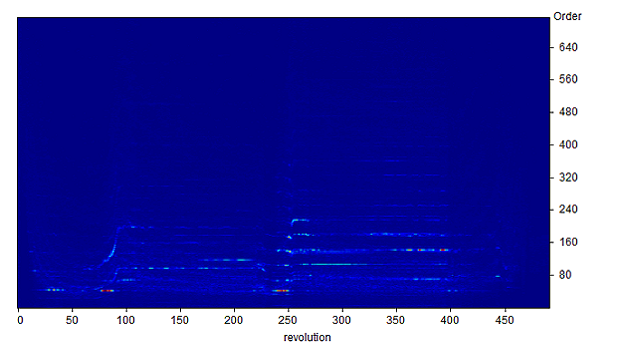
Instead of displaying the Y-axis in Hz (oscillations per second), this graphic shows it in "Order" units ("oscillations per shaft revolution"). The order of 1 means "the same frequency as the shaft", the order of 2 means "2x shaft frequency" etc.
For most visible artefacts in the spectrogram, you can observe a straight track for each order, indicating that the vibration occurs at a fixed multiple of the motor rotational speed.
Inverse order transformation
After generating the order-signal, you can work with it just as with any other time-domain signal. For example, you can perform one of the filtering functions. Please note that all frequency related functions refer to revolutions/orders instead of "Hz".
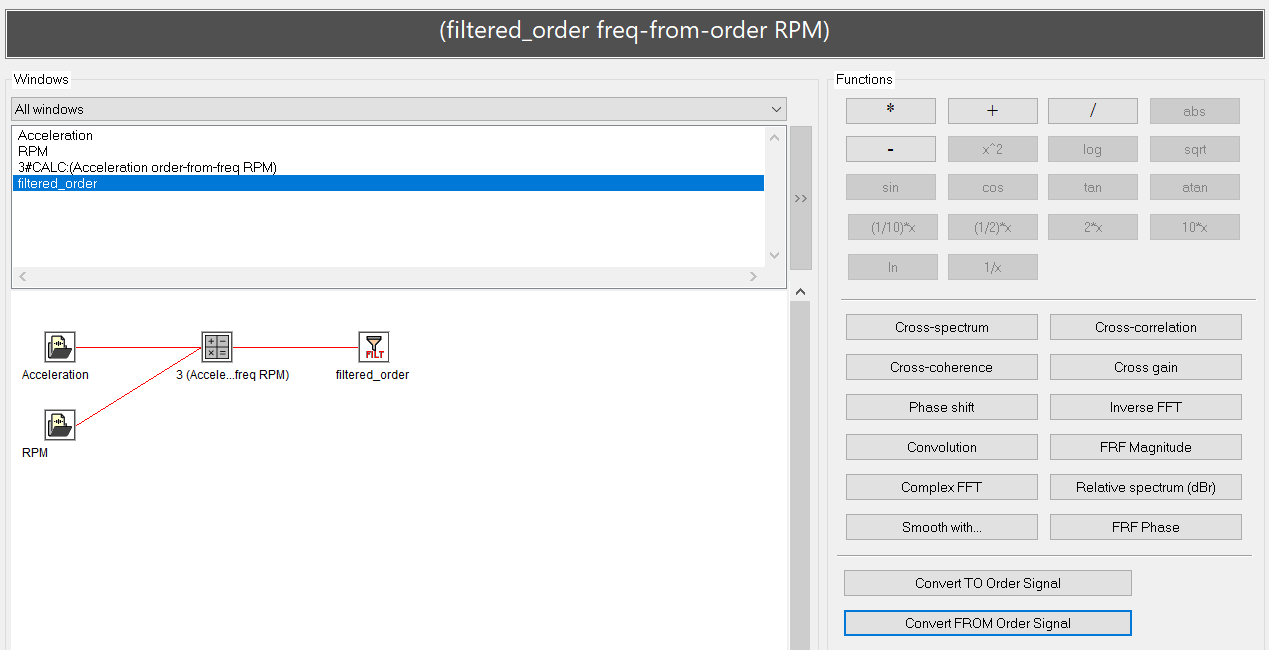
For example, you could filter the main shaft frequency and all its harmonics out of the order-signal and then convert the order-signal back to the time-signal again.
You can perform this inverse transformation by using the Signal calculator and its function "Convert FROM Order signal". You will have to choose the RPM signal used to calculate the order-signal as a second parameter again. The result of this operation will be a time-domain signal again.
Links
For more information about this technique, see some of these external links:
https://en.wikipedia.org/wiki/Order_tracking_(signal_processing)
https://www.mathworks.com/help/signal/examples/order-analysis-of-a-vibration-signal.html
